317. Μη μετωπική ελαστική κρούση m1 και m2 και μέγιστη γωνία εκτροπής (2).

 Σφαίρα μάζας m₂=4m₁ κινείται με ταχύτητα υ₂=9m/s και συγκρούεται μη μετωπικά και ελαστικά με σφαίρα m₁ που κινείται με ταχύτητα υ₁=4m/s. Να υπολογίσετε τη μέγιστη γωνία εκτροπής της m₁ μετά την κρούση.....

Συνοπτική λύση:

316. Σφαίρα σε οριζόντια επίπεδα (2).

 Ομογενής σφαίρα μάζας m=2Kg και ακτίνας R=10cm ηρεμεί αρχικά πάνω σε οριζόντιο επίπεδο σε σημείο Α. Κάποια στιγμή (t=0), εξασκείται στο κέντρο μάζας Κ της σφαίρας,  σταθερή οριζόντια δύναμη F=14N όπως φαίνεται στο σχήμα. Η σφαίρα τότε αρχίζει να κυλίεται χωρίς να ολισθαίνει με επιτάχυνση α_cm=5m/s².

Όταν η σφαίρα διανύσει απόσταση (ΑΒ)= x₁=1,6m συναντάει λείο οριζόντιο επίπεδο ΒΓ, με (ΒΓ)=x₂=6m και συνεχίζει να κινείται  πάνω σ’ αυτό, οπότε κάποια στιγμή φτάνει στο σημείο Γ

A) α) Να υπολογιστεί η στατική τριβή Τ_στ για την κίνηση της σφαίρας από το Α μέχρι το Β.

β) Όταν η σφαίρα κινείται στο λείο οριζόντιο επίπεδο ΒΓ να δείξετε ότι τότε, η γωνιακή ταχύτητά της παραμένει σταθερή ενώ η μεταφορική της ταχύτητα αυξάνεται.

Β) Καθώς η σφαίρα φτάνει στο σημείο Γ, συναντάει ένα οριζόντιο επίπεδο με συντελεστή τριβής ολίσθησης μ=0,8 και συνεχίζει να κινείται πάνω σ’ αυτό. Αν μετά το Γ η γωνιακή επιτάχυνση της σφαίρας είναι σταθερή και ίση με α_γων=200rad/s², τότε σε πόσο χρόνο t₁ από τη στιγμή που συναντάει η σφαίρα το οριζόντιο αυτό επίπεδο αρχίζει η κύλισή της;

Γ) Να υπολογιστεί ο συνολικός ρυθμός μεταβολής της στροφορμής της σφαίρας  σε κάθε επίπεδο κίνησης.

Συνοπτική λύση:

315. Κυκλική κίνηση ηλεκτρικού φορτίου και εκπομπή ακτινοβολίας

Ένα επιταχυνόμενο ηλεκτρικό φορτίο με επιτάχυνση α,  σύμφωνα με την ηλεκτρομαγνητική θεωρία εκπέμπει ακτινοβολία – ενέργεια με τη μορφή ηλεκτρομαγνητικού κύματος. Ο ρυθμός ροής της ενέργειας (ισχύς ανά μονάδα επιφάνειας), σε ένα ηλεκτρομαγνητικό κύμα, δίνεται από το διάνυσμα Poynting:

  ...συνέχεια

314. Ισορροπία και ανατροπή σφαίρας

 

Η σφαίρα του σχήματος είναι ομογενής και έχει μάζα m=1Kg.

Στη σφαίρα ασκούνται οι δυο δυνάμεις του σχήματος στα σημεία Ζ και Ε που είναι ίσες με F και έχουν τη φορά του σχήματος. Η σφαίρα μπορεί να υπερπηδήσει είτε το σκαλοπάτι Α, είτε το σκαλοπάτι Β.

Α) Να υπολογιστεί η ακτίνα της σφαίρας αν δίνεται ότι (ΑΒ)=120cm και h=40cm.

Β ) Αν δίνονται (ΚΕ)=40cm και (ΚΖ)=50cm, τότε ως προς ποιο σημείο Α ή Β είναι δυνατόν να ανατραπεί η σφαίρα; Ποιά είναι τότε η ελάχιστη τιμή της F;

Γ) Να υπολογιστεί η δύναμη που δέχεται τότε αυτή στα σημεία επαφής Α και Β.

Δίνεται g=10m/s².

Συνοπτική λύση:

313. Αυτεπαγωγή και παράλληλη σύνδεση

 

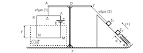
Για το κύκλωμα του σχήματος δίνονται Ε=120V, r=5 Ω, R₁=60Ω, R₂=10Ω. Το σωληνοειδές είναι μη ιδανικό με R_Σ=20Ω και   L=0,1  H. Ακόμη το σωληνοειδές έχει Ν=1000 σπείρες και μήκος l=1m.

A) Τη χρονική στιγμή t₀=0 κλείνουμε το διακόπτη δ. Τότε εκείνη τη στιγμή να υπολογίσετε τις εντάσεις των ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές.

 B) Να υπολογίσετε τις εντάσεις των ηλεκτρικών ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, μόλις το κύκλωμα έρθει σε μόνιμη κατάσταση τη χρονική στιγμή t₁.

 Γ) Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, κάποια χρονική στιγμή t₂ πριν το κύκλωμα έρθει σε μόνιμη κατάσταση για την οποία η ένταση του ρεύματος που διαρρέει το σωληνοειδές είναι Ι_Σ=0,5 Α.

 Δ) Αφού το κύκλωμα έχει έρθει σε μόνιμη κατάσταση κάποια χρονική στιγμή t_3>t₁, ανοίγουμε το διακόπτη. Εκείνη τη στιγμή (t₃), να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές. Στη συνέχεια να υπολογίσετε τις τελικές εντάσεις των ηλεκτρικών ρευμάτων.

 Ε) Με το διακόπτη δ κλειστό πριν το κύκλωμα έρθει σε μόνιμη κατάσταση και όταν η συνολική ένταση που διαρρέει το κύκλωμα είναι Ι=2 Α ανοίγουμε το διακόπτη. Εκείνη τη στιγμή (t₂), να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές.

Δίνεται: μ₀=4π·10^-7N/A².

 Συνοπτική λύση: