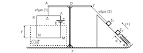
Μια ράβδος ΑΒ, που θεωρείται αβαρής και έχει μήκος L=0,8m μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο, γύρω από άξονα που περνά από το σημείο της Ο. Το σημείο Ο απέχει από το άκρο της Α απόσταση (ΟΑ)=0,2m. Επίσης στο σημείο Γ της ράβδου με (ΒΓ)=(ΟΑ) υπάρχει στερεωμένη σημειακή μάζα m= 1Kg. Αρχικά η ράβδος ισορροπεί σε κατακόρυφη θέση ώστε το άκρο της Β να βρίσκεται κάτω από τον άξονα περιστροφής.
Μια δεύτερη σημειακή μάζα m, κινείται οριζόντια με σταθερή ταχύτητα υ και συγκρούεται με τη μάζα m που βρίσκεται στο Γ. Αν η κρούση θεωρηθεί ελαστική και ότι η μάζα m τόσο πριν όσο και μετά την κρούση κινείται οριζόντια, τότε να υπολογιστεί η τιμή της ταχύτητας υ, ώστε να πετύχουμε οριακή ανακύκλωση της ράβδου.
Δίνεται g=10m/s2.
Συνοπτική λύση:















Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου