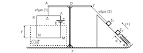
Στο κύκλωμα του
σχήματος η ράβδος ΚΛ, έχει ωμική αντίσταση RΚΛ=R=1Ω, μήκος L=1m, και μάζα m=0,5Κg.
Τη χρονική στιγμή t0=0
ασκούμε στο μέσο της ράβδου μια σταθερή οριζόντια δύναμη
F. Τότε η ράβδος
αρχίζει να ολισθαίνει χωρίς τριβές ενώ βρίσκεται συνέχεια σε επαφή με δυο παράλληλους μεταλλικούς αγωγούς Αx και Ay αμελητέας αντίστασης όπως στο σχήμα. Η ράβδος κινείται μέσα σε ομογενές μαγνητικό πεδίο έντασης (μαγνητικής επαγωγής) Β=1T, που είναι κάθετο στο επίπεδο κίνησης της ράβδου. Τα άκρα Α και Γ των μεταλλικών αγωγών συνδέονται με ιδανικό πηνίο με συντελεστή αυτεπαγωγής L=0,5H, το οποίο βρίσκεται έξω από το ομογενές μαγνητικό πεδίο. Λόγω της κίνησης της ράβδου ο βρόχος ΚΛΓΑΚ διαρρέεται από ρεύμα Ι=2t. Τότε από τη χρονική στιγμή t0=0 και μέχρι τη χρονική στιγμή t=2s να υπολογίσετε το συνολικό ηλεκτρικό φορτίο που διέρχεται από μια διατομή του κυκλώματος.
Συνοπτική λύση:















Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου