322. Ταλάντωση και επαγωγική τάση

 

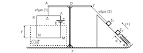
Στο κύκλωμα του σχήματος η ηλεκτρική πηγή έχει στοιχεία Ε=20 V και r=2Ω. Ο διακόπτης δ είναι αρχικά κλειστός και η ομογενής ράβδος (ΛΜ) που έχει ωμική αντίσταση R=8Ω, μήκος L=1m και μάζα m=0,1Kg, ισορροπεί σε οριζόντια θέση όπως στο σχήμα.

Η ράβδος είναι δεμένη στο μέσο της από το ελεύθερο άκρο ιδανικού  ελατηρίου σταθεράς Κ=200Ν/m, το άλλο άκρο του οποίου είναι δεμένο σε σταθερό σημείο. Ακόμη η ράβδος  μπορεί να ολισθαίνει χωρίς τριβές στους κατακόρυφους μεταλλικούς στύλους ΑΛ και ΓΜ. Το ελατήριο είναι αρχικά επιμηκυμένο, ενώ η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης (μαγνητικής επαγωγής) Β=1

T, που είναι κάθετο στο επίπεδο των αγωγών με τη φορά του σχήματος. Τότε:

Α) Να υπολογιστεί η αρχική επιμήκυνση του ελατηρίου.

Β) Τη χρονική στιγμή t₀=0 ανοίγουμε το διακόπτη.

i)   Να αποδείξετε τότε ότι η ράβδος πραγματοποιεί α.α.τ και

ii) Να βρείτε πως μεταβάλλεται με το χρόνο η τάση από επαγωγή στα άκρα της ράβδου και να κάνετε την αντίστοιχη γραφική παράσταση. Θεωρείστε για την ταλάντωση την προς τα πάνω φορά θετική.

Γ) Να υπολογιστούν: ο ρυθμός μεταβολής της κινητικής ενέργειας, και ο ρυθμός μεταβολής της βαρυτικής δυναμικής ενέργειας της ράβδου. Τι παρατηρείτε;

Δίνεται για τις πράξεις g=10m/s².

 Συνοπτική λύση: