241. Κύλιση με ολίσθηση (κατά την άνοδο σε πλάγιο επίπεδο)

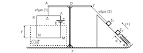
Σφαίρα μάζας m=7Kg και ακτίνας R=0,2m αρχικά κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο με υ₀=8m/s. Κάποια στιγμή (t=0), φτάνει στη βάση κεκλιμένου επιπέδου γωνίας κλίσης φ με ημφ=0,8 και συνφ=0,6 και αρχίζει να ανέρχεται σε αυτό. Αν ο συντελεστής τριβής ολίσθησης που τον θεωρούμε ίσο με το συντελεστή στατικής τριβής μεταξύ της σφαίρας και του κεκλιμένου επιπέδου είναι μ= τότε:

α) Τι είδους κίνηση θα κάνει η σφαίρα στο κεκλιμένο επίπεδο;

β) Σε πόσο χρόνο θα ισχύει υ_cm=0,72υ_γρ, όπου υ_cm είναι η ταχύτητα του κέντρου μάζας της σφαίρας και υ_γρ είναι η γραμμική ταχύτητα των σημείων της περιφέρειάς της;

γ) Να υπολογιστεί το έργο της τριβής ολίσθησης κατά την κίνηση της σφαίρας στο κεκλιμένο επίπεδο για τον παραπάνω χρόνο.

δ) Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας και ο ρυθμός μεταβολής της στροφορμής της σφαίρας την παραπάνω χρονική στιγμή.

Δίνεται για τη σφαίρα και για άξονα περιστροφής που περνάει από το κέντρο μάζας της Ι=×m×R²  =∙7∙0,04=0,112 Κg∙m² και g=10m/s².

Συνοπτική λύση:

ή εδώ