334. Σύνθετη κίνηση ράβδου σε ομογενές μαγνητικό πεδίο Β.

 

Η αγώγιμη ράβδος ΚΛ του σχήματος έχει μήκος (ΚΛ)=L=0,5m και περιστρέφεται με σταθερή γωνιακή ταχύτητα ω=40 rad/s, γύρω από το άκρο της Κ και με τη φορά που φαίνεται στο σχήμα. Το ομογενές μαγνητικό πεδίο έχει ένταση Β=0,4T και είναι κάθετο στο επίπεδο κίνησης της ράβδου. Κάποια χρονική στιγμή (t₀=0),  η ράβδος αρχίζει να κινείται με σταθερή οριζόντια ταχύτητα υ=10m/s. Εκείνη τη στιγμή η ράβδος ΚΛ είναι οριζόντια και έχει τη διεύθυνση της υ. Τότε να υπολογιστεί σε συνάρτηση με το χρόνο η στιγμιαία τιμή της τάσης V_K-V_Λ=V_ΚΛ(t).

 Συνοπτική λύση:

333. Ομογενής ράβδος που ισορροπεί οριακά(2)

 

Λεπτή ομογενής ράβδος ΑΒ μήκους L=1,6m και μάζας m=3Kg, είναι ακουμπισμένη σε λείο
κατακόρυφο τοίχο ενώ το  του μήκους της προεξέχει από ένα σκαλοπάτι όπως φαίνεται στο σχήμα και η ράβδος ισορροπεί.

Α) Αν ο συντελεστής στατικής τριβής ανάμεσα  στη ράβδο και το σκαλοπάτι είναι μ=root3, να βρεθεί  η τιμή της γωνίας φ,  που πρέπει να σχηματίζει η ράβδος με το σκαλοπάτι ώστε η ράβδος να μη γλιστρά.

Β) Στο σημείο Γ στηρίζουμε τη ράβδο μ’ ένα μεντεσέ ώστε αυτή να μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο. Κάποια στιγμή τοποθετούμε πάνω στη σανίδα και στο άκρο της Β, έναν κύλινδρο μάζας Μ=8Κg οποίος κυλίεται χωρίς να ολισθαίνει. Να βρείτε σε ποια απόσταση από το Γ πρέπει να βρίσκεται ο κύλινδρος καθώς κατέρχεται ώστε η σανίδα μόλις να περιστραφεί (ανατραπεί).

Αν η επιτάχυνση του κέντρου μάζας του κυλίνδρου καθώς κατέρχεται είναι α_cm=10/3m/s², τότε ποια είναι εκείνη τη στιγμή η ταχύτητα του κυλίνδρου και πόσο χρόνο διαρκεί η κίνηση του κυλίνδρου πάνω στη ράβδο μέχρι τη στιγμή που ανατρέπεται;

Δίνεται g=10m/s².

 Συνοπτική λύση:

332. Fελ και απλή αρμονική ταλάντωση.

 Σώμα μάζας m είναι δεμένο σε κατακόρυφο ελατήριο σταθεράς Κ και πραγματοποιεί απλή αρμονική ταλάντωση.  Η γραφική παράσταση της δύναμης του ελατηρίου σε συνάρτηση με την απομάκρυνση x  από τη θέση ισορροπίας φαίνεται στο παρακάτω σχήμα.Nα βρείτε την εξίσωση της απομάκρυνσης x, σε συνάρτηση με το χρόνο t. Θεωρείστε ότι δεν υπάρχει αρχική φάση φ₀. Δίνεται g=10m/s².

Συνοπτική λύση:

331. Φωτοηλεκτρικό φαινόμενο και de Broglie

 

Στη διάταξη μελέτης του φωτοηλεκτρικού φαινομένου, που φαίνεται στο διπλανό σχήμα χρησιμοποιείται πηγή μονοχρωματικής ακτινοβολίας που εκπέμπει φωτόνια μήκους κύματος  λ = 600nm. Η ακτινοβολία πέφτει στην επιφάνεια  της καθόδου (Κ) που αποτελείται από επίστρωση οξειδίου του Cs. Το έργο εξαγωγής της καθόδου είναι φ=13·10^-20J  τότε:

 A) Να υπολογίσετε τη μέγιστη κινητική ενέργεια Κ_max, με την οποία εγκαταλείπουν το μέταλλο της καθόδου τα φωτοηλεκτρόνια.

 B) Να υπολογιστεί το μήκος κύματος (λ_e),  κα
τά de Broglie των φωτοηλεκτρονίων.

 Γ) Nα υπολογιστεί η συχνότητα αυτών των φωτοηλεκτρονίων.

Δίνονται: η σταθερά του Planck h=6,6∙10^-34J∙s, η ταχύτητα του φωτός c=3∙10⁸m/s, η μάζα m, του ηλεκτρονίου m=9·10^-31Kg  και 1eV=1,6∙10^-19J.

 Συνοπτική λύση:

περισσότερα εδώ

330. Κίνηση τριγωνικού πλαισίου σε ομογενές μαγνητικό πεδίο Β.

 

Το συρμάτινο αγώγιμο πλαίσιο ΚΛΜ του σχήματος έχει τη μορφή ισόπλευρου τριγώνου πλευράς α=2m. Το πλαίσιο ολισθαίνει με σταθερή οριζόντια ταχύτητα υ=root3m/s κατά μήκος του ύψους του ΛΡ. Τη χρονική στιγμή t₀=0 το πλαίσιο αρχίζει να εισέρχεται σε κατακόρυφο ομογενές μαγνητικό πεδίο Β=2T πλάτους d=root6m.

Να εκφράσετε την ΗΕΔ από επαγωγή στο πλαίσιο σε συνάρτηση με το χρόνο t.

 Συνοπτική λύση:

329. Κίνηση ράβδου σε ομογενές μαγνητικό πεδίο Β.

 

Η αγώγιμη ράβδος ΚΛ του σχήματος έχει μήκος (ΚΛ)=L=1,2m και παρουσιάζει ωμική αντίσταση R^*=5Ω/m. Οι αγωγοί Αx και Ay σχηματίζουν γωνία φ=45⁰. Η ράβδος κινείται με σταθερή ταχύτητα υ=0,2m/s και ξεκινάει αρχικά (t₀=0) από τη θέση Α. Η κίνηση γίνεται χωρίς τριβές και η ράβδος εφάπτεται συνεχώς στους αγωγούς Αx και Γy ενώ είναι κάθετη στο σύρμα Αx στο σημείο Λ.   Οι αγωγοί Αx και Αy δεν παρουσιάζουν ωμική αντίσταση.

Ακόμη η κίνηση γίνεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο Β=1T, όπως στο σχήμα. Τότε:

Α) Να υπολογίσετε την ένταση Ι του ηλεκτρικού ρεύματος σε συνάρτηση με το χρόνο t και να υπολογίστε το ολικό φορτίο για όσο χρόνο διαρκεί η κίνηση.

Β) Να βρείτε τη δύναμη Lapace σε συνάρτηση με το χρόνο και να υπολογίσετε τη θερμότητα που αναπτύσσεται στο κύκλωμα στον παραπάνω χρόνο.

Γ) Να υπολογίσετε τη διαφορά δυναμικού V_K-V_Λ τη χρονική στιγμή t=5s.

Δ)Να υπολογίσετε τη συνολική μεταβολή της μαγνητικής ροής ΔΦ.

Συνοπτική λύση:

328. Νόμος Biot - Savart σε ευθύγραμμο λεπτό ρευματοφόρο αγωγό

 

Έστω το ευθύγραμμο σύρμα ΚΛ, που διαρρέεται από ρεύμα Ι. Για να υπολογίσουμε το μαγνητικό πεδίο που δημιουργεί ο αγωγός στο τυχαίο σημείο Α, που απέχει απόσταση α, από τον αγωγό, χωρίζουμε τον αγωγό σε πολύ μικρά τμήματα. Έστω ένα τέτοιο τμήμα μήκους Δl, που απέχει απόσταση r από το σημείο Α. Το μικρό αυτό τμήμα δημιουργεί στο σημείο Α μαγνητικό πεδίο που από το Νόμο των Biot και Savart έχει μέτρο........

Συνοπτική λύση:

327. Νόμος Biot - Savart σε τόξο

Αγωγός σχήματος τόξου, κύκλου κέντρου Ο και ακτίνας r= m, έχει μήκος (ΓΔ)= S, που αντιστοιχεί σε γωνία φ=150⁰, και διαρρέεται από ρεύμα Ι=2Α. Τότε να υπολογιστεί το μέτρο της έντασης του μαγνητικού του πεδίου Β στο κέντρο Ο.

Συνοπτική λύση:

326. tολ σε ηλεκτρικό και μαγνητικό πεδίο

 

Σωματίδιο
μάζας m=3·10^-10Kg, έχει ηλεκτρικό φορτίο q=+1μC και εισέρχεται σε ομογενές ηλεκτρικό πεδίο έντασης Ε=100V/m κάθετα στις ηλεκτρικές δυναμικές γραμμές με οριζόντια ταχύτητα υ₀=100m/s. Το σωματίδιο εξέρχεται από το ηλεκτρικό πεδίο με ταχύτητα 2υ₀ και αμέσως εισέρχεται σε ομογενές μαγνητικό πεδίο μαγνητικής επαγωγής Β=π/10T κάθετα στις δυναμικές του γραμμές. Στη συνέχεια μέσα στο μαγνητικό πεδίο διαγράφει τόξο (ΓΔ) μήκους S και εξέρχεται από αυτό.

Να υπολογιστεί ο συνολικός χρόνος κίνησης του σωματιδίου στα δυο πεδία δυνάμεων.

Συνοπτική λύση:

Κρούσεις...από το μπιλιάρδο στο διάστημα

 

Κρούσεις: Το παρεχόμενο κείμενο αποτελείται από αποσπάσματα του κεφαλαίου "ΚΡΟΥΣΕΙΣ" ενός σχολικού εγχειριδίου Φυσικής Γ' Λυκείου Κατεύθυνσης, γραμμένο από τον ΜΙΧΑΗΛ Π. ΜΙΧΑΗΛ. Το υλικό εξετάζει λεπτομερώς τις κρούσεις τόσο στη μηχανική του μακρόκοσμου (π.χ., μπάλες μπιλιάρδου) όσο και στην ατομική και πυρηνική φυσική (σκέδαση σωματιδίων), όπου η επαφή δεν είναι απαραίτητη. Κεντρικοί άξονες της ανάλυσης είναι η αρχή διατήρησης της ορμής, η οποία ισχύει πάντα στις κρούσεις, και η ενέργεια στις κρούσεις, η οποία διατηρείται μόνο στις ελαστικές κρούσεις. Επιπλέον, το κείμενο ταξινομεί τις κρούσεις με βάση τη γεωμετρία τους (κεντρικές, έκκεντρες, πλάγιες) και περιλαμβάνει αναλυτικά παραδείγματα και ασκήσεις τόσο για ελαστικές όσο και για ανελαστικές/πλαστικές κρούσεις, όπως η περίπτωση της συγκόλλησης σωμάτων.

  Το ηχητικό εδώ

To video εδώ

pdf

foto1

foto2

325. Ράβδος και στρεφόμενο πλαίσιο

 

Αβαρής ράβδος ΑΓ έχει μήκος L=0,8m, και ισορροπεί αρχικά  σε οριζόντια θέση. Στο άκρο Γ της ράβδου υπάρχει αβαρές τετράγωνο πλαίσιο πλευράς α=0,1m στις κορυφές του οποίου υπάρχουν αντίστοιχα τέσσερις σημειακές μάζες m=1Kg. Το πλαίσιο στρέφεται κατά τη φορά των δεικτών του ρολογιού, σε κατακόρυφο επίπεδο και γύρω από οριζόντιο άξονα που περνά από το κέντρο του, που ταυτίζεται με το άκρο Γ της ράβδου όπως φαίνεται στο σχήμα. H σταθερή γωνιακή ταχύτητα περιστροφής του πλαισίου είναι ω_π=10rad/s. Στη συνέχεια αφήνουμε το σύστημα ελεύθερο να περιστραφεί χωρίς τριβές γύρω από το άκρο Α της ράβδου. Να υπολογιστούν:

α) Η αρχική στροφορμή του συστήματος των τεσσάρων μαζών ως προς τον άξονα περιστροφής στο σημείο Α και

β) Η στροφορμή του συστήματος ως προς τον άξονα περιστροφής τη στιγμή που καθώς περιστρέφεται βρίσκεται στην κατακόρυφη θέση.

Δίνεται η επιτάχυνση της βαρύτητας g=10m/s².

Συνοπτική λύση:

324. Μέγιστη κινητική ενέργεια

 Σφαίρα μάζας m₁  πέφτει με ταχύτητα υ₁ σε ακίνητη σφαίρα μάζας m₂ και συγκρούεται ελαστικά και κεντρικά με αυτή. Ποια πρέπει να είναι η σχέση μεταξύ των m₁ και m₂ ώστε μετά την κρούση  η σφαίρα m₂ να έχει μέγιστη κινητική ενέργεια;

 Συνοπτική Λύση:

323. Ταλάντωση και νήμα

 

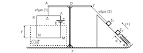
Στο κατακόρυφο ελατήριο του σχήματος σταθεράς Κ=100N/m, έχουμε δέσει το σώμα μάζας Μ=1Κg ενώ μέσω αβαρούς νήματος το έχουμε συνδέσει με τη σφαίρα μάζας m=3Kg.

Απομακρύνουμε το σύστημα των δυο σωμάτων κατακόρυφα προς τα κάτω κατά Α=0,2m και αφήνουμε το σύστημα να ταλαντωθεί.

α) Να δείξετε ότι το σύστημα θα πραγματοποιήσει α.α.τ.

β) Να κάνετε τη γραφική παράσταση της τάσης του νήματος T(x) σε συνάρτηση με την απομάκρυνση από τη θέση ισορροπίας.

γ) Να κάνετε τη γραφική παράσταση της τάσης του νήματος T(t) σε συνάρτηση με το χρόνο. Θεωρήστε την προς τα κάτω φορά θετική.

δ) Για ποιο πλάτος ταλάντωσης η τάση του νήματος μηδενίζεται;

ε) Αν το όριο θραύσης του νήματος είναι Τ_θρ=330Ν, τότε για ποια συχνότητα ταλάντωσης κόβεται το νήμα στη θέση x=0,25m από τη θέση ισορροπίας; Θεωρήστε ότι έχουμε επιλέξει κατάλληλο πλάτος ταλάντωσης. Δίνεται g=10m/s².

 Συνοπτική λύση:

322. Ταλάντωση και επαγωγική τάση

 

Στο κύκλωμα του σχήματος η ηλεκτρική πηγή έχει στοιχεία Ε=20 V και r=2Ω. Ο διακόπτης δ είναι αρχικά κλειστός και η ομογενής ράβδος (ΛΜ) που έχει ωμική αντίσταση R=8Ω, μήκος L=1m και μάζα m=0,1Kg, ισορροπεί σε οριζόντια θέση όπως στο σχήμα.

Η ράβδος είναι δεμένη στο μέσο της από το ελεύθερο άκρο ιδανικού  ελατηρίου σταθεράς Κ=200Ν/m, το άλλο άκρο του οποίου είναι δεμένο σε σταθερό σημείο. Ακόμη η ράβδος  μπορεί να ολισθαίνει χωρίς τριβές στους κατακόρυφους μεταλλικούς στύλους ΑΛ και ΓΜ. Το ελατήριο είναι αρχικά επιμηκυμένο, ενώ η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης (μαγνητικής επαγωγής) Β=1

T, που είναι κάθετο στο επίπεδο των αγωγών με τη φορά του σχήματος. Τότε:

Α) Να υπολογιστεί η αρχική επιμήκυνση του ελατηρίου.

Β) Τη χρονική στιγμή t₀=0 ανοίγουμε το διακόπτη.

i)   Να αποδείξετε τότε ότι η ράβδος πραγματοποιεί α.α.τ και

ii) Να βρείτε πως μεταβάλλεται με το χρόνο η τάση από επαγωγή στα άκρα της ράβδου και να κάνετε την αντίστοιχη γραφική παράσταση. Θεωρείστε για την ταλάντωση την προς τα πάνω φορά θετική.

Γ) Να υπολογιστούν: ο ρυθμός μεταβολής της κινητικής ενέργειας, και ο ρυθμός μεταβολής της βαρυτικής δυναμικής ενέργειας της ράβδου. Τι παρατηρείτε;

Δίνεται για τις πράξεις g=10m/s².

 Συνοπτική λύση:

321. Ισορροπία και μετά ταλάντωση

 Ο στερεός κύλινδρος του σχήματος μάζας m=4Kg και ακτίνας R, ισορροπεί σε κεκλιμένο επίπεδο γωνίας κλίσης φ με ημφ=0,6 και συνφ=0,8 δεμένος με νήμα. Η άλλη άκρη του νήματος είναι δεμένη επίσης σε μάζα m και αυτή με ελατήριο σταθεράς Κ=D=400N/m όπως φαίνεται στο σχήμα. Αν το οριζόντιο επίπεδο είναι λείο, τότε:

α) Να υπολογιστεί η τάση του νήματος και η συνολική δύναμη που δέχεται ο κύλινδρος από το κεκλιμένο επίπεδο. Για ποιες τιμές του συντελεστή στατικής τριβής ο κύλινδρος ισορροπεί;  

β) Τη χρονική στιγμή t=0 κόβουμε το νήμα. Τότε εκείνη τη στιγμή να υπολογιστεί η επιτάχυνση του σώματος που είναι αρχικά δεμένο στο ελατήριο.

γ) Το σώμα m, μόλις βρεθεί στη Θ.Ι με θετική ταχύτητα για πρώτη φορά αποκολλάται από το ελατήριο. Τότε να γίνει η γραφική παράσταση της ορμής του σε συνάρτηση με το χρόνο και για χρόνο t=0,3π s, από τη στιγμή που κόψαμε το νήμα.

 δ) Να γίνει η γραφική παράσταση του ρυθμού μεταβολής της κινητικής ενέργειας του σώματος για τον παραπάνω χρόνο. Θεωρείστε την προς τ’ αριστερά φορά θετική.

 Για τις πράξεις g=10m/s².

 

Συνοπτική λύση:

320. Στάσιμο κύμα.

Σε γραμμικό ομογενές ελαστικό μέσο, μεγάλου μήκους διαδίδονται δυο αρμονικά κύματα, τα οποία δημιουργούν στάσιμο κύμα και περιγράφονται από τις εξισώσεις y₁=0,4×ημ2π(5t-x/2) και y₂=0,4×ημ2π(5t+x/2+3/4).

α) Να γράψετε την εξίσωση του στάσιμου κύματος που σχηματίζεται μετά τη συμβολή των κυμάτων. Θεωρούμε ότι το στάσιμο κύμα δημιουργήθηκε τη χρονική στιγμή t₀=0.

β) Να βρείτε τις θέσεις των δεσμών και των κοιλιών του στάσιμου κύματος, από την αρχή Ο (x₀=0), του συστήματος συντεταγμένων. Ποια είναι η απόσταση μεταξύ δυο διαδοχικών δεσμών ή κοιλιών του στάσιμου κύματος;

γ) Για ένα σημείο Μ του ελαστικού μέσου που έχει πλάτος ταλάντωσης 0,4root3m, να βρείτε τη μικρότερή του απόσταση από την αρχή Ο, και να κάνετε τη γραφική παράσταση της απομάκρυνσής του, της ταχύτητας ταλάντωσής του καθώς και του πλάτους του σε συνάρτηση με το χρόνο t.

δ) Να σχεδιάσετε το στιγμιότυπο του στάσιμου κύματος τη χρονική στιγμή t=3/20 s και για την περιοχή -2£x£3m του ελαστικού μέσου διάδοσης.

ε) Να γίνει η γραφική παράσταση του πλάτους |Α΄| του στάσιμου κύματος σε συνάρτηση με το x και για -2£x£3m.

 Συνοπτική λύση:

Φορά διάδοσης κύματος

 Στο σχήμα έχουμε ένα τμήμα ενός στιγμιότυπου ενός αρμονικού κύματος τη χρονική στιγμή t₁. Το κύμα διαδίδεται στον άξονα x΄x με σταθερή ταχύτητα υ=10m/s. Αν τη χρονική στιγμή t₁ η φάση του σημείου K είναι  φ_Κ=5π rad τότε:

α) να βρεθεί η φορά διάδοσης του κύματος,

β) να βρεθεί η εξίσωση του κύματος, αν το σημείο Λ αρχίζει να ταλαντώνεται τη χρονική στιγμή t=0, ενώ το κύμα εκτείνεται στο υπερπέραν,

γ) να σχεδιαστεί το στιγμιότυπο του κύματος τη χρονική στιγμή t₁.

 
Συνοπτική λύση:  

και εδώ

Κρούση και αποθηκευμένη ενέργεια

 Σώμα μάζας m=1Kg κινείται με ταχύτητα υ₀ και  συγκρούεται κεντρικά με αρχικά ακίνητο σώμα μάζας M=4Kg.

Κατά την κρούση ενέργεια Ε=2,5J αποθηκεύεται στο σύστημα των δυο μαζών. Ποια πρέπει να είναι τότε η ελάχιστη τιμή της ταχύτητας υ₀  του σώματος μάζας m;

 

Συνοπτική λύση:

Μη μετωπική ελαστική κρούση m1 και m2 και μέγιστη γωνία εκτροπής.

Μια σφαίρα μάζας m1 κινείται με ταχύτητα υ1=4m/s και συγκρούεται μη μετωπικά και ελαστικά με σφαίρα μάζας m2 με m2=4m1, που κινείται με ταχύτητα υ2=9m/s.

Τότε:

α) Να υπολογίσετε τη μέγιστη γωνία εκτροπής της m1.
β) Για τη γωνία εκτροπής που υπολογίσατε να βρείτε τις ταχύτητες υ1 και υ2 των δυο μαζών m1 και m2 αντίστοιχα, μετά την κρούση.

Συνοπτική λύση:

ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Λυκείου ΑΡΙΣΤΟΤΕΛΗΣ 2025 – B΄ Τάξη

 

Δίνεται το κύκλωμα του σχήματος, όπου 𝑅 = root5-1𝛺. Οι διακεκομμένες γραμμές στα σημεία Κ και Λ υπονοούν ότι το τμήμα του κυκλώματος που οριοθετείται από το πλαίσιο επαναλαμβάνεται προς τα δεξιά 𝛮 φορές με 𝛮 ≫ 1). Να υπολογίσετε την ολική αντίσταση 𝑅𝜊𝜆 της συνδεσμολογίας.

Συνοπτική λύση:

319. …και κεντρική και πλάγια πλαστική κρούση

Σώμα μάζας m₁=2Kg κινείται με ταχύτητα υ₁=20m/s που σχηματίζει με τον ορίζοντα γωνία φ=60⁰. Ένα δεύτερο σώμα m₂=3Kg κινείται οριζόντια με ταχύτητα υ₂=10m/s. Τα σώματα σφηνώνονται ακαριαία σε  αρχικά ακίνητο σώμα μάζας Μ=5Kg,  που ισορροπεί σε λείο οριζόντιο επίπεδο. Αν το συσσωμάτωμα μετά την κρούση κινείται οριζόντια τότε, να υπολογιστούν:

 α) η κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση.

β) η μεταβολή της ορμής της κάθε μάζας κατά τη διάρκεια της κρούσης.

γ) το ποσοστό απώλειας της κινητικής ενέργειας του συστήματος των τριών μαζών.

δ) ο ρυθμός μεταβολής της δυναμικής ενέργειας της m₁ πριν να σφηνωθεί στη μάζα M.

Συνοπτική λύση:

318. Αυτεπαγωγή και πυκνωτής

 Για το κύκλωμα του σχήματος δίνονται Ε=120V, r=5 Ω, R₁=15Ω, R₂=10Ω. Το σωληνοειδές είναι μη ιδανικό με R_Σ=5Ω και   L=5mH, ενώ ο πυκνωτής έχει χωρητικότητα C=1mF.

A) Τη χρονική στιγμή t₀=0 κλείνουμε το διακόπτη δ. Να υπολογίσετε τις εντάσεις των ηλεκτρικών ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, μόλις το κύκλωμα έρθει σε μόνιμη κατάσταση τη χρονική στιγμή t₁.

 Β)Αφού το κύκλωμα έρθει σε μόνιμη κατάσταση κάποια χρονική στιγμή t_3>t₁, ανοίγουμε το διακόπτη δ. Να υπολογίσετε τη συνολική θερμική ενέργεια που αναπτύσσεται λόγω φαινομένου Joule στον αντιστάτη R₁. Στη συνέχεια να υπολογίσετε τις τελικές εντάσεις των ηλεκτρικών ρευμάτων.

 Συνοπτική λύση:

239. Στάσιμο κύμα και διάγραμμα φάσης

Κατά μήκος ομογενούς οριζόντιας χορδής έχει σχηματιστεί στάσιμο κύμα. Παρακάτω φαίνεται το στιγμιότυπο του κύματος κάποια χρονική στιγμή t που η κινητική ενέργεια της χορδής είναι μηδενική. Τα σημεία Α και Β της χορδής είναι δεσμοί και απέχουν μεταξύ τους απόσταση L.

Η αρχή των αξόνων(Ο) βρίσκεται στο μέσο της απόστασης ΑΒ και το σημείο αυτό βρίσκεται τη χρονική στιγμή t=0 στη θέση ισορροπίας του κινούμενο κατά τη θετική φορά. Ο χρόνος που μεσολαβεί ανάμεσα σε δυο διαδοχικές μεγιστοποιήσεις της δυναμικής ενέργειας της χορδής είναι 0,25 s. Η μικρότερη απόσταση ανάμεσα σε δυο κοιλίες με διαφορά φάσης 0 rad είναι 2m. Το πλάτος ταλάντωσης ενός σημείου (Μ) που βρίσκεται στη θέση x=+2L/15 είναι Α_Μ=0,1 m.

Να γίνει το διάγραμμα της φάσης φ των σημείων της χορδής σε συνάρτηση με τη θέση τους x τη χρονική στιγμή t=1/8 s και τη χρονική στιγμή t=1s.

 

Συνοπτική λύση:

209. Στάσιμο κύμα. x=0 κοιλία ή δεσμός;

 Κατά μήκος γραμμικού ομογενούς ελαστικού μέσου, το οποίο εκτείνεται κατά τη διεύθυνση x΄x, δημιουργείται στάσιμο κύμα. Oι εξισώσεις των δυο τρεχόντων κυμάτων  που με τη συμβολή τους δημιούργησαν το στάσιμο κύμα είναι,

y₁=A ημ2π(t/T-x/λ+φ0/2π)   και y₂= A ημ2π(t/T+x/λ). Ποια είναι τότε η μικρότερη κατά απόλυτη τιμή αρχική φάση φ₀, ώστε μετά τη συμβολή των δυο κυμάτων κατά μήκος της χορδής το σημείο x=0 να έχει πλάτος:

i)                    2Α,  δηλαδή να είναι κοιλία του στάσιμου κύματος

ii)                   0,  δηλαδή να είναι δεσμός του στάσιμου κύματος

iii)                 Α;

 Συνοπτική λύση:  

154. Ενέργεια και στάσιμο κύμα

 Κατά μήκος χορδής      μήκους L=17,5cm και μάζας Μ=0,2 Kg, διαδίδονται

ταυτόχρονα δυο αρμονικά κύματα. Από τη συμβολή των δυο κυμάτων προκύπτει το στάσιμο κύμα y=0,02 συν(20πx)ημ(40πt) (S.I)  (t=0, x=0, y=0, v>0).

Να  σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή 1/200s.

Τι είδους ενέργεια έχουν τα μόρια της χορδής εκείνη τη στιγμή; Να την υπολογίσετε. 

 Δίνεται π²=10.

Συνοπτική λύση:

172. Διαφορά φάσης και στιγμιότυπο κύματος.

 Σημείο Μ του ελαστικού μέσου διάδοσης ενός κύματος βρίσκεται στη θέση x_M και ταλαντώνεται με συχνότητα f=2Hz. Το Μ, έχει διαφορά φάσης κατά 2π rad μικρότερη από την «πηγή» (εφόσον το κύμα έχει «φτάσει» ήδη στο Μ).

 Α) Πόση πρέπει να γίνει η συχνότητα της πηγής ώστε η διαφορά φάσης του Μ με την «πηγή» Ο να γίνει:

i)                    4π rad και

ii)                    π rad;

 Β) Να σχεδιάσετε τα στιγμιότυπα του κύματος τη χρονική στιγμή t=1 s για

      i)    Δφ=2π rad

      ii)   Δφ=4π rad και

iii)                Δφ=π rad;

 Δίνεται η ταχύτητα διάδοσης του κύματος υ=2m/s.

 Συνοπτική λύση:

171. Διάδοση κύματος

Η διαφορική εξίσωση του κύματος ή απλή κυματική εξίσωση είναι:

Μια λύση της παραπάνω κυματικής εξίσωσης έχει τη μορφή y(x,t)=f(x-υt), όπου f είναι μια τυχαία διπλά παραγωγίσιμη συνάρτηση της μεταβλητής (x-υt).

 Η εξίσωση y(x,t)=f(x-υt), είναι η γενική εξίσωση που παριστάνει ένα κύμα οποιουδήποτε σχήματος που κινείται προς τον θετικό ημιάξονα +x.

 Τη μορφή της διαταραχής, δηλαδή τη χωρική μεταβολή του κύματος, μπορούμε να τη «δούμε», αν φωτογραφήσουμε το κύμα σε μια ορισμένη χρονική στιγμή. Αυτό σημαίνει ότι θα  πρέπει να δώσουμε μια συγκεκριμένη τιμή π.χ  t= t₁ στο χρόνο, οπότε έχουμε το στιγμιότυπο του κύματος που είναι μια συνάρτηση μόνο του x, για τη δεδομένη χρονική στιγμή δηλαδή  τη συνάρτηση f(x)= y(x,t₁).......

η συνέχεια εδώ

317. Μη μετωπική ελαστική κρούση m1 και m2 και μέγιστη γωνία εκτροπής (2).

 Σφαίρα μάζας m₂=4m₁ κινείται με ταχύτητα υ₂=9m/s και συγκρούεται μη μετωπικά και ελαστικά με σφαίρα m₁ που κινείται με ταχύτητα υ₁=4m/s. Να υπολογίσετε τη μέγιστη γωνία εκτροπής της m₁ μετά την κρούση.....

Συνοπτική λύση:

316. Σφαίρα σε οριζόντια επίπεδα (2).

 Ομογενής σφαίρα μάζας m=2Kg και ακτίνας R=10cm ηρεμεί αρχικά πάνω σε οριζόντιο επίπεδο σε σημείο Α. Κάποια στιγμή (t=0), εξασκείται στο κέντρο μάζας Κ της σφαίρας,  σταθερή οριζόντια δύναμη F=14N όπως φαίνεται στο σχήμα. Η σφαίρα τότε αρχίζει να κυλίεται χωρίς να ολισθαίνει με επιτάχυνση α_cm=5m/s².

Όταν η σφαίρα διανύσει απόσταση (ΑΒ)= x₁=1,6m συναντάει λείο οριζόντιο επίπεδο ΒΓ, με (ΒΓ)=x₂=6m και συνεχίζει να κινείται  πάνω σ’ αυτό, οπότε κάποια στιγμή φτάνει στο σημείο Γ

A) α) Να υπολογιστεί η στατική τριβή Τ_στ για την κίνηση της σφαίρας από το Α μέχρι το Β.

β) Όταν η σφαίρα κινείται στο λείο οριζόντιο επίπεδο ΒΓ να δείξετε ότι τότε, η γωνιακή ταχύτητά της παραμένει σταθερή ενώ η μεταφορική της ταχύτητα αυξάνεται.

Β) Καθώς η σφαίρα φτάνει στο σημείο Γ, συναντάει ένα οριζόντιο επίπεδο με συντελεστή τριβής ολίσθησης μ=0,8 και συνεχίζει να κινείται πάνω σ’ αυτό. Αν μετά το Γ η γωνιακή επιτάχυνση της σφαίρας είναι σταθερή και ίση με α_γων=200rad/s², τότε σε πόσο χρόνο t₁ από τη στιγμή που συναντάει η σφαίρα το οριζόντιο αυτό επίπεδο αρχίζει η κύλισή της;

Γ) Να υπολογιστεί ο συνολικός ρυθμός μεταβολής της στροφορμής της σφαίρας  σε κάθε επίπεδο κίνησης.

Συνοπτική λύση:

315. Κυκλική κίνηση ηλεκτρικού φορτίου και εκπομπή ακτινοβολίας

Ένα επιταχυνόμενο ηλεκτρικό φορτίο με επιτάχυνση α,  σύμφωνα με την ηλεκτρομαγνητική θεωρία εκπέμπει ακτινοβολία – ενέργεια με τη μορφή ηλεκτρομαγνητικού κύματος. Ο ρυθμός ροής της ενέργειας (ισχύς ανά μονάδα επιφάνειας), σε ένα ηλεκτρομαγνητικό κύμα, δίνεται από το διάνυσμα Poynting:

  ...συνέχεια