324. Μέγιστη κινητική ενέργεια

 Σφαίρα μάζας m₁  πέφτει με ταχύτητα υ₁ σε ακίνητη σφαίρα μάζας m₂ και συγκρούεται ελαστικά και κεντρικά με αυτή. Ποια πρέπει να είναι η σχέση μεταξύ των m₁ και m₂ ώστε μετά την κρούση  η σφαίρα m₂ να έχει μέγιστη κινητική ενέργεια;

 Συνοπτική Λύση:

323. Ταλάντωση και νήμα

 

Στο κατακόρυφο ελατήριο του σχήματος σταθεράς Κ=100N/m, έχουμε δέσει το σώμα μάζας Μ=1Κg ενώ μέσω αβαρούς νήματος το έχουμε συνδέσει με τη σφαίρα μάζας m=3Kg.

Απομακρύνουμε το σύστημα των δυο σωμάτων κατακόρυφα προς τα κάτω κατά Α=0,2m και αφήνουμε το σύστημα να ταλαντωθεί.

α) Να δείξετε ότι το σύστημα θα πραγματοποιήσει α.α.τ.

β) Να κάνετε τη γραφική παράσταση της τάσης του νήματος T(x) σε συνάρτηση με την απομάκρυνση από τη θέση ισορροπίας.

γ) Να κάνετε τη γραφική παράσταση της τάσης του νήματος T(t) σε συνάρτηση με το χρόνο. Θεωρήστε την προς τα κάτω φορά θετική.

δ) Για ποιο πλάτος ταλάντωσης η τάση του νήματος μηδενίζεται;

ε) Αν το όριο θραύσης του νήματος είναι Τ_θρ=330Ν, τότε για ποια συχνότητα ταλάντωσης κόβεται το νήμα στη θέση x=0,25m από τη θέση ισορροπίας; Θεωρήστε ότι έχουμε επιλέξει κατάλληλο πλάτος ταλάντωσης. Δίνεται g=10m/s².

 Συνοπτική λύση:

322. Ταλάντωση και επαγωγική τάση

 

Στο κύκλωμα του σχήματος η ηλεκτρική πηγή έχει στοιχεία Ε=20 V και r=2Ω. Ο διακόπτης δ είναι αρχικά κλειστός και η ομογενής ράβδος (ΛΜ) που έχει ωμική αντίσταση R=8Ω, μήκος L=1m και μάζα m=0,1Kg, ισορροπεί σε οριζόντια θέση όπως στο σχήμα.

Η ράβδος είναι δεμένη στο μέσο της από το ελεύθερο άκρο ιδανικού  ελατηρίου σταθεράς Κ=200Ν/m, το άλλο άκρο του οποίου είναι δεμένο σε σταθερό σημείο. Ακόμη η ράβδος  μπορεί να ολισθαίνει χωρίς τριβές στους κατακόρυφους μεταλλικούς στύλους ΑΛ και ΓΜ. Το ελατήριο είναι αρχικά επιμηκυμένο, ενώ η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης (μαγνητικής επαγωγής) Β=1

T, που είναι κάθετο στο επίπεδο των αγωγών με τη φορά του σχήματος. Τότε:

Α) Να υπολογιστεί η αρχική επιμήκυνση του ελατηρίου.

Β) Τη χρονική στιγμή t₀=0 ανοίγουμε το διακόπτη.

i)   Να αποδείξετε τότε ότι η ράβδος πραγματοποιεί α.α.τ και

ii) Να βρείτε πως μεταβάλλεται με το χρόνο η τάση από επαγωγή στα άκρα της ράβδου και να κάνετε την αντίστοιχη γραφική παράσταση. Θεωρείστε για την ταλάντωση την προς τα πάνω φορά θετική.

Γ) Να υπολογιστούν: ο ρυθμός μεταβολής της κινητικής ενέργειας, και ο ρυθμός μεταβολής της βαρυτικής δυναμικής ενέργειας της ράβδου. Τι παρατηρείτε;

Δίνεται για τις πράξεις g=10m/s².

 Συνοπτική λύση:

321. Ισορροπία και μετά ταλάντωση

 Ο στερεός κύλινδρος του σχήματος μάζας m=4Kg και ακτίνας R, ισορροπεί σε κεκλιμένο επίπεδο γωνίας κλίσης φ με ημφ=0,6 και συνφ=0,8 δεμένος με νήμα. Η άλλη άκρη του νήματος είναι δεμένη επίσης σε μάζα m και αυτή με ελατήριο σταθεράς Κ=D=400N/m όπως φαίνεται στο σχήμα. Αν το οριζόντιο επίπεδο είναι λείο, τότε:

α) Να υπολογιστεί η τάση του νήματος και η συνολική δύναμη που δέχεται ο κύλινδρος από το κεκλιμένο επίπεδο. Για ποιες τιμές του συντελεστή στατικής τριβής ο κύλινδρος ισορροπεί;  

β) Τη χρονική στιγμή t=0 κόβουμε το νήμα. Τότε εκείνη τη στιγμή να υπολογιστεί η επιτάχυνση του σώματος που είναι αρχικά δεμένο στο ελατήριο.

γ) Το σώμα m, μόλις βρεθεί στη Θ.Ι με θετική ταχύτητα για πρώτη φορά αποκολλάται από το ελατήριο. Τότε να γίνει η γραφική παράσταση της ορμής του σε συνάρτηση με το χρόνο και για χρόνο t=0,3π s, από τη στιγμή που κόψαμε το νήμα.

 δ) Να γίνει η γραφική παράσταση του ρυθμού μεταβολής της κινητικής ενέργειας του σώματος για τον παραπάνω χρόνο. Θεωρείστε την προς τ’ αριστερά φορά θετική.

 Για τις πράξεις g=10m/s².

 

Συνοπτική λύση:

320. Στάσιμο κύμα.

Σε γραμμικό ομογενές ελαστικό μέσο, μεγάλου μήκους διαδίδονται δυο αρμονικά κύματα, τα οποία δημιουργούν στάσιμο κύμα και περιγράφονται από τις εξισώσεις y₁=0,4×ημ2π(5t-x/2) και y₂=0,4×ημ2π(5t+x/2+3/4).

α) Να γράψετε την εξίσωση του στάσιμου κύματος που σχηματίζεται μετά τη συμβολή των κυμάτων. Θεωρούμε ότι το στάσιμο κύμα δημιουργήθηκε τη χρονική στιγμή t₀=0.

β) Να βρείτε τις θέσεις των δεσμών και των κοιλιών του στάσιμου κύματος, από την αρχή Ο (x₀=0), του συστήματος συντεταγμένων. Ποια είναι η απόσταση μεταξύ δυο διαδοχικών δεσμών ή κοιλιών του στάσιμου κύματος;

γ) Για ένα σημείο Μ του ελαστικού μέσου που έχει πλάτος ταλάντωσης 0,4root3m, να βρείτε τη μικρότερή του απόσταση από την αρχή Ο, και να κάνετε τη γραφική παράσταση της απομάκρυνσής του, της ταχύτητας ταλάντωσής του καθώς και του πλάτους του σε συνάρτηση με το χρόνο t.

δ) Να σχεδιάσετε το στιγμιότυπο του στάσιμου κύματος τη χρονική στιγμή t=3/20 s και για την περιοχή -2£x£3m του ελαστικού μέσου διάδοσης.

ε) Να γίνει η γραφική παράσταση του πλάτους |Α΄| του στάσιμου κύματος σε συνάρτηση με το x και για -2£x£3m.

 Συνοπτική λύση:

Φορά διάδοσης κύματος

 Στο σχήμα έχουμε ένα τμήμα ενός στιγμιότυπου ενός αρμονικού κύματος τη χρονική στιγμή t₁. Το κύμα διαδίδεται στον άξονα x΄x με σταθερή ταχύτητα υ=10m/s. Αν τη χρονική στιγμή t₁ η φάση του σημείου K είναι  φ_Κ=5π rad τότε:

α) να βρεθεί η φορά διάδοσης του κύματος,

β) να βρεθεί η εξίσωση του κύματος, αν το σημείο Λ αρχίζει να ταλαντώνεται τη χρονική στιγμή t=0, ενώ το κύμα εκτείνεται στο υπερπέραν,

γ) να σχεδιαστεί το στιγμιότυπο του κύματος τη χρονική στιγμή t₁.

 
Συνοπτική λύση:  

και εδώ

Κρούση και αποθηκευμένη ενέργεια

 Σώμα μάζας m=1Kg κινείται με ταχύτητα υ₀ και  συγκρούεται κεντρικά με αρχικά ακίνητο σώμα μάζας M=4Kg.

Κατά την κρούση ενέργεια Ε=2,5J αποθηκεύεται στο σύστημα των δυο μαζών. Ποια πρέπει να είναι τότε η ελάχιστη τιμή της ταχύτητας υ₀  του σώματος μάζας m;

 

Συνοπτική λύση:

Μη μετωπική ελαστική κρούση m1 και m2 και μέγιστη γωνία εκτροπής.

Μια σφαίρα μάζας m1 κινείται με ταχύτητα υ1=4m/s και συγκρούεται μη μετωπικά και ελαστικά με σφαίρα μάζας m2 με m2=4m1, που κινείται με ταχύτητα υ2=9m/s.

Τότε:

α) Να υπολογίσετε τη μέγιστη γωνία εκτροπής της m1.
β) Για τη γωνία εκτροπής που υπολογίσατε να βρείτε τις ταχύτητες υ1 και υ2 των δυο μαζών m1 και m2 αντίστοιχα, μετά την κρούση.

Συνοπτική λύση:

ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Λυκείου ΑΡΙΣΤΟΤΕΛΗΣ 2025 – B΄ Τάξη

 

Δίνεται το κύκλωμα του σχήματος, όπου 𝑅 = root5-1𝛺. Οι διακεκομμένες γραμμές στα σημεία Κ και Λ υπονοούν ότι το τμήμα του κυκλώματος που οριοθετείται από το πλαίσιο επαναλαμβάνεται προς τα δεξιά 𝛮 φορές με 𝛮 ≫ 1). Να υπολογίσετε την ολική αντίσταση 𝑅𝜊𝜆 της συνδεσμολογίας.

Συνοπτική λύση:

319. …και κεντρική και πλάγια πλαστική κρούση

Σώμα μάζας m₁=2Kg κινείται με ταχύτητα υ₁=20m/s που σχηματίζει με τον ορίζοντα γωνία φ=60⁰. Ένα δεύτερο σώμα m₂=3Kg κινείται οριζόντια με ταχύτητα υ₂=10m/s. Τα σώματα σφηνώνονται ακαριαία σε  αρχικά ακίνητο σώμα μάζας Μ=5Kg,  που ισορροπεί σε λείο οριζόντιο επίπεδο. Αν το συσσωμάτωμα μετά την κρούση κινείται οριζόντια τότε, να υπολογιστούν:

 α) η κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση.

β) η μεταβολή της ορμής της κάθε μάζας κατά τη διάρκεια της κρούσης.

γ) το ποσοστό απώλειας της κινητικής ενέργειας του συστήματος των τριών μαζών.

δ) ο ρυθμός μεταβολής της δυναμικής ενέργειας της m₁ πριν να σφηνωθεί στη μάζα M.

Συνοπτική λύση:

318. Αυτεπαγωγή και πυκνωτής

 Για το κύκλωμα του σχήματος δίνονται Ε=120V, r=5 Ω, R₁=15Ω, R₂=10Ω. Το σωληνοειδές είναι μη ιδανικό με R_Σ=5Ω και   L=5mH, ενώ ο πυκνωτής έχει χωρητικότητα C=1mF.

A) Τη χρονική στιγμή t₀=0 κλείνουμε το διακόπτη δ. Να υπολογίσετε τις εντάσεις των ηλεκτρικών ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, μόλις το κύκλωμα έρθει σε μόνιμη κατάσταση τη χρονική στιγμή t₁.

 Β)Αφού το κύκλωμα έρθει σε μόνιμη κατάσταση κάποια χρονική στιγμή t_3>t₁, ανοίγουμε το διακόπτη δ. Να υπολογίσετε τη συνολική θερμική ενέργεια που αναπτύσσεται λόγω φαινομένου Joule στον αντιστάτη R₁. Στη συνέχεια να υπολογίσετε τις τελικές εντάσεις των ηλεκτρικών ρευμάτων.

 Συνοπτική λύση:

239. Στάσιμο κύμα και διάγραμμα φάσης

Κατά μήκος ομογενούς οριζόντιας χορδής έχει σχηματιστεί στάσιμο κύμα. Παρακάτω φαίνεται το στιγμιότυπο του κύματος κάποια χρονική στιγμή t που η κινητική ενέργεια της χορδής είναι μηδενική. Τα σημεία Α και Β της χορδής είναι δεσμοί και απέχουν μεταξύ τους απόσταση L.

Η αρχή των αξόνων(Ο) βρίσκεται στο μέσο της απόστασης ΑΒ και το σημείο αυτό βρίσκεται τη χρονική στιγμή t=0 στη θέση ισορροπίας του κινούμενο κατά τη θετική φορά. Ο χρόνος που μεσολαβεί ανάμεσα σε δυο διαδοχικές μεγιστοποιήσεις της δυναμικής ενέργειας της χορδής είναι 0,25 s. Η μικρότερη απόσταση ανάμεσα σε δυο κοιλίες με διαφορά φάσης 0 rad είναι 2m. Το πλάτος ταλάντωσης ενός σημείου (Μ) που βρίσκεται στη θέση x=+2L/15 είναι Α_Μ=0,1 m.

Να γίνει το διάγραμμα της φάσης φ των σημείων της χορδής σε συνάρτηση με τη θέση τους x τη χρονική στιγμή t=1/8 s και τη χρονική στιγμή t=1s.

 

Συνοπτική λύση:

209. Στάσιμο κύμα. x=0 κοιλία ή δεσμός;

 Κατά μήκος γραμμικού ομογενούς ελαστικού μέσου, το οποίο εκτείνεται κατά τη διεύθυνση x΄x, δημιουργείται στάσιμο κύμα. Oι εξισώσεις των δυο τρεχόντων κυμάτων  που με τη συμβολή τους δημιούργησαν το στάσιμο κύμα είναι,

y₁=A ημ2π(t/T-x/λ+φ0/2π)   και y₂= A ημ2π(t/T+x/λ). Ποια είναι τότε η μικρότερη κατά απόλυτη τιμή αρχική φάση φ₀, ώστε μετά τη συμβολή των δυο κυμάτων κατά μήκος της χορδής το σημείο x=0 να έχει πλάτος:

i)                    2Α,  δηλαδή να είναι κοιλία του στάσιμου κύματος

ii)                   0,  δηλαδή να είναι δεσμός του στάσιμου κύματος

iii)                 Α;

 Συνοπτική λύση:  

154. Ενέργεια και στάσιμο κύμα

 Κατά μήκος χορδής      μήκους L=17,5cm και μάζας Μ=0,2 Kg, διαδίδονται

ταυτόχρονα δυο αρμονικά κύματα. Από τη συμβολή των δυο κυμάτων προκύπτει το στάσιμο κύμα y=0,02 συν(20πx)ημ(40πt) (S.I)  (t=0, x=0, y=0, v>0).

Να  σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή 1/200s.

Τι είδους ενέργεια έχουν τα μόρια της χορδής εκείνη τη στιγμή; Να την υπολογίσετε. 

 Δίνεται π²=10.

Συνοπτική λύση:

172. Διαφορά φάσης και στιγμιότυπο κύματος.

 Σημείο Μ του ελαστικού μέσου διάδοσης ενός κύματος βρίσκεται στη θέση x_M και ταλαντώνεται με συχνότητα f=2Hz. Το Μ, έχει διαφορά φάσης κατά 2π rad μικρότερη από την «πηγή» (εφόσον το κύμα έχει «φτάσει» ήδη στο Μ).

 Α) Πόση πρέπει να γίνει η συχνότητα της πηγής ώστε η διαφορά φάσης του Μ με την «πηγή» Ο να γίνει:

i)                    4π rad και

ii)                    π rad;

 Β) Να σχεδιάσετε τα στιγμιότυπα του κύματος τη χρονική στιγμή t=1 s για

      i)    Δφ=2π rad

      ii)   Δφ=4π rad και

iii)                Δφ=π rad;

 Δίνεται η ταχύτητα διάδοσης του κύματος υ=2m/s.

 Συνοπτική λύση:

171. Διάδοση κύματος

Η διαφορική εξίσωση του κύματος ή απλή κυματική εξίσωση είναι:

Μια λύση της παραπάνω κυματικής εξίσωσης έχει τη μορφή y(x,t)=f(x-υt), όπου f είναι μια τυχαία διπλά παραγωγίσιμη συνάρτηση της μεταβλητής (x-υt).

 Η εξίσωση y(x,t)=f(x-υt), είναι η γενική εξίσωση που παριστάνει ένα κύμα οποιουδήποτε σχήματος που κινείται προς τον θετικό ημιάξονα +x.

 Τη μορφή της διαταραχής, δηλαδή τη χωρική μεταβολή του κύματος, μπορούμε να τη «δούμε», αν φωτογραφήσουμε το κύμα σε μια ορισμένη χρονική στιγμή. Αυτό σημαίνει ότι θα  πρέπει να δώσουμε μια συγκεκριμένη τιμή π.χ  t= t₁ στο χρόνο, οπότε έχουμε το στιγμιότυπο του κύματος που είναι μια συνάρτηση μόνο του x, για τη δεδομένη χρονική στιγμή δηλαδή  τη συνάρτηση f(x)= y(x,t₁).......

η συνέχεια εδώ

317. Μη μετωπική ελαστική κρούση m1 και m2 και μέγιστη γωνία εκτροπής (2).

 Σφαίρα μάζας m₂=4m₁ κινείται με ταχύτητα υ₂=9m/s και συγκρούεται μη μετωπικά και ελαστικά με σφαίρα m₁ που κινείται με ταχύτητα υ₁=4m/s. Να υπολογίσετε τη μέγιστη γωνία εκτροπής της m₁ μετά την κρούση.....

Συνοπτική λύση:

316. Σφαίρα σε οριζόντια επίπεδα (2).

 Ομογενής σφαίρα μάζας m=2Kg και ακτίνας R=10cm ηρεμεί αρχικά πάνω σε οριζόντιο επίπεδο σε σημείο Α. Κάποια στιγμή (t=0), εξασκείται στο κέντρο μάζας Κ της σφαίρας,  σταθερή οριζόντια δύναμη F=14N όπως φαίνεται στο σχήμα. Η σφαίρα τότε αρχίζει να κυλίεται χωρίς να ολισθαίνει με επιτάχυνση α_cm=5m/s².

Όταν η σφαίρα διανύσει απόσταση (ΑΒ)= x₁=1,6m συναντάει λείο οριζόντιο επίπεδο ΒΓ, με (ΒΓ)=x₂=6m και συνεχίζει να κινείται  πάνω σ’ αυτό, οπότε κάποια στιγμή φτάνει στο σημείο Γ

A) α) Να υπολογιστεί η στατική τριβή Τ_στ για την κίνηση της σφαίρας από το Α μέχρι το Β.

β) Όταν η σφαίρα κινείται στο λείο οριζόντιο επίπεδο ΒΓ να δείξετε ότι τότε, η γωνιακή ταχύτητά της παραμένει σταθερή ενώ η μεταφορική της ταχύτητα αυξάνεται.

Β) Καθώς η σφαίρα φτάνει στο σημείο Γ, συναντάει ένα οριζόντιο επίπεδο με συντελεστή τριβής ολίσθησης μ=0,8 και συνεχίζει να κινείται πάνω σ’ αυτό. Αν μετά το Γ η γωνιακή επιτάχυνση της σφαίρας είναι σταθερή και ίση με α_γων=200rad/s², τότε σε πόσο χρόνο t₁ από τη στιγμή που συναντάει η σφαίρα το οριζόντιο αυτό επίπεδο αρχίζει η κύλισή της;

Γ) Να υπολογιστεί ο συνολικός ρυθμός μεταβολής της στροφορμής της σφαίρας  σε κάθε επίπεδο κίνησης.

Συνοπτική λύση:

315. Κυκλική κίνηση ηλεκτρικού φορτίου και εκπομπή ακτινοβολίας

Ένα επιταχυνόμενο ηλεκτρικό φορτίο με επιτάχυνση α,  σύμφωνα με την ηλεκτρομαγνητική θεωρία εκπέμπει ακτινοβολία – ενέργεια με τη μορφή ηλεκτρομαγνητικού κύματος. Ο ρυθμός ροής της ενέργειας (ισχύς ανά μονάδα επιφάνειας), σε ένα ηλεκτρομαγνητικό κύμα, δίνεται από το διάνυσμα Poynting:

  ...συνέχεια

314. Ισορροπία και ανατροπή σφαίρας

 

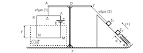
Η σφαίρα του σχήματος είναι ομογενής και έχει μάζα m=1Kg.

Στη σφαίρα ασκούνται οι δυο δυνάμεις του σχήματος στα σημεία Ζ και Ε που είναι ίσες με F και έχουν τη φορά του σχήματος. Η σφαίρα μπορεί να υπερπηδήσει είτε το σκαλοπάτι Α, είτε το σκαλοπάτι Β.

Α) Να υπολογιστεί η ακτίνα της σφαίρας αν δίνεται ότι (ΑΒ)=120cm και h=40cm.

Β ) Αν δίνονται (ΚΕ)=40cm και (ΚΖ)=50cm, τότε ως προς ποιο σημείο Α ή Β είναι δυνατόν να ανατραπεί η σφαίρα; Ποιά είναι τότε η ελάχιστη τιμή της F;

Γ) Να υπολογιστεί η δύναμη που δέχεται τότε αυτή στα σημεία επαφής Α και Β.

Δίνεται g=10m/s².

Συνοπτική λύση:

313. Αυτεπαγωγή και παράλληλη σύνδεση

 

Για το κύκλωμα του σχήματος δίνονται Ε=120V, r=5 Ω, R₁=60Ω, R₂=10Ω. Το σωληνοειδές είναι μη ιδανικό με R_Σ=20Ω και   L=0,1  H. Ακόμη το σωληνοειδές έχει Ν=1000 σπείρες και μήκος l=1m.

A) Τη χρονική στιγμή t₀=0 κλείνουμε το διακόπτη δ. Τότε εκείνη τη στιγμή να υπολογίσετε τις εντάσεις των ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές.

 B) Να υπολογίσετε τις εντάσεις των ηλεκτρικών ρευμάτων στο κύκλωμα καθώς και το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, μόλις το κύκλωμα έρθει σε μόνιμη κατάσταση τη χρονική στιγμή t₁.

 Γ) Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές, κάποια χρονική στιγμή t₂ πριν το κύκλωμα έρθει σε μόνιμη κατάσταση για την οποία η ένταση του ρεύματος που διαρρέει το σωληνοειδές είναι Ι_Σ=0,5 Α.

 Δ) Αφού το κύκλωμα έχει έρθει σε μόνιμη κατάσταση κάποια χρονική στιγμή t_3>t₁, ανοίγουμε το διακόπτη. Εκείνη τη στιγμή (t₃), να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές. Στη συνέχεια να υπολογίσετε τις τελικές εντάσεις των ηλεκτρικών ρευμάτων.

 Ε) Με το διακόπτη δ κλειστό πριν το κύκλωμα έρθει σε μόνιμη κατάσταση και όταν η συνολική ένταση που διαρρέει το κύκλωμα είναι Ι=2 Α ανοίγουμε το διακόπτη. Εκείνη τη στιγμή (t₂), να υπολογίσετε το ρυθμό μεταβολής της έντασης του ηλεκτρικού ρεύματος που διαρρέει το σωληνοειδές.

Δίνεται: μ₀=4π·10^-7N/A².

 Συνοπτική λύση:

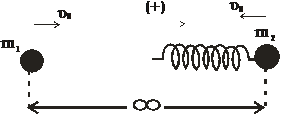
312. Κρούση και δυναμική ενέργεια

Δυο μάζες m₁=1Kg και m₂=3m₁, βρίσκονται αρχικά σε άπειρη μεταξύ τους απόσταση ώστε να μην αλληλεπιδρούν. Στη μάζα m₂, έχουμε προσαρμόσει κατάλληλα ένα ιδανικό αβαρές ελατήριο σταθεράς Κ=300Ν/m, όπως φαίνεται στο σχήμα. Κάποια στιγμή εκτοξεύουμε ταυτόχρονα στην ίδια ευθεία τις δυο μάζες τη μια εναντίον της άλλης με ίσες ταχύτητες μέτρου υ₀=12m/s . Τότε:

 Α) Να υπολογίσετε τις ταχύτητες των δυο μαζών όταν βρεθούν στην ελάχιστη μεταξύ τους απόσταση. Πόση είναι η μέγιστη μεταβολή της κινητικής ενέργειας του συστήματος των δυο μαζών; Πόση είναι η μέγιστη συμπίεση του ελατηρίου;

 Β) Να υπολογίσετε τις ταχύτητές τους όταν τελικά βρεθούν σε θέσεις όπου πάλι δεν αλληλεπιδρούν μεταξύ τους.

 
Γ) Να σχεδιάσετε το διάγραμμα της μεταβολής της κινητικής ενέργειας σε συνάρτηση με το χρόνο ΔΚ(t), για το σύστημα των μαζών από την αρχή και μέχρι να βρεθούν ξανά σε θέσεις όπου δεν αλληλεπιδρούν μεταξύ τους.

 

Συνοπτική λύση:

Νόμος του Ampere

Ampere

Νόμος της ηλεκτρομαγνητικής επαγωγής του Faraday

 

Faraday

310. Louis de Broglie (Αρχή του κυματοσωματιδιακού δυϊσμού).

 

Ο Louis de  Broglie (1923), πιστεύοντας στη συμμετρία της φύσης υπέθεσε ότι, όχι μόνο το φωτόνιο αλλά και κάθε κινούμενο σωματίδιο έχει και κυματικές ιδιότητες. Τα πειράματα περίθλασης δέσμης ηλεκτρονίων, που κινούνται με μεγάλη ταχύτητα (Davisson – Germer), έδειξαν ότι και αυτά περιθλώνται όπως ακριβώς τα φωτόνια (ακτίνες Χ), άρα είναι λογικό να υποθέσουμε ότι έχουν και κυματική συμπεριφορά. Παρόμοια πειράματα έγιναν και με σωμάτια α καθώς και με νετρόνια με τα ίδια αποτελέσματα. Γενικά  λοιπόν ένα  κινούμενο  σωματίδιο με ταχύτητα υ όπως ένα ηλεκτρόνιο, έχει ορμή p και ενέργεια Ε που σχετίζεται με ένα υλικό κύμα, που έχει μήκος κύματος λ και συχνότητα f και ισχύουν:λ=h/p.........................

Συνέχεια:

309. Διαφορά φάσης Ε, Β σε ηλεκτρομαγνητικό κύμα κατά την ελεύθερη διάδοσή του στο χώρο.

Έστω ηλεκτρομαγνητικό κύμα που διαδίδεται προς τα δεξιά με ταχύτητα c. Για παρατηρητή μακριά από την πηγή, οι ισοφασικές επιφάνεις που ορίζονται τα ηλεκτρικά (Ε) και τα μαγνητικά (Β) πεδία που φτάνουν σε αυτόν είναι επίπεδα και το κύμα που περνά από αυτόν λέμε ότι είναι επίπεδο κύμα. Στο σχήμα φαίνεται δυο ισοφασικές επιφάνειες του στιγμιότυπου του κύματος που διαδίδεται κατά τον άξονα των x. Ακόμη το Ε είναι παράλληλο στον άξονα yy΄ και το Β είναι παράλληλο στον άξονα zz΄................................

συνέχεια

308. Κίνηση σε ομογενές μαγνητικό και ηλεκτρικό πεδίο

 Α)Το ομογενές μαγνητικό πεδίο του σχήματος είναι κατακόρυφο,  κάθετο στο επίπεδο της σελίδας με τη φορά που φαίνεται στο σχήμα και έχει μέτρο Β=0,2T, ενώ εκτείνεται  σε περιοχή μήκους d.

Σωματίδιο μάζας m=10^-6Kg και φορτίου q=10mC εκτοξεύεται τη χρονική στιγμή t₀=0 από το σημείο Α οριζόντια με ταχύτητα υ₀=200m/s. Το σωματίδιο εξέρχεται από το μαγνητικό πεδίο, έχοντας διαγράψει τροχιά μήκους (ΑΛ)=S=π/60m. 

Τότε να υπολογιστούν:

Α1. Ο χρόνος κίνησης Δt του ηλεκτρικού φορτίου στο μαγνητικό πεδίο.

A2. Η απόκλιση y του ηλεκτρικού φορτίου από την ευθύγραμμη διάδοσή του τη στιγμή που βγαίνει από το πεδίο.

Α3. Το μήκος d του πεδίου.

Α4. Η μεταβολή του μέτρου της ορμής του ηλεκτρικού φορτίου καθώς και το μέτρο της μεταβολής της ορμής του κατά την κίνησή του στο μαγνητικό πεδίο. Πόσο είναι το έργο της δύναμης Lorentz κατά την κίνηση του φορτίου;

 Β) Αν στον ίδιο χώρο  καταργήσουμε το μαγνητικό πεδίο Β και δημιουργήσουμε ένα οριζόντιο ομογενές ηλεκτρικό πεδίο έντασης Ε=0,2V/m όπως στο σχήμα, τότε να υπολογιστούν:

Β1. Ο χρόνος κίνησης Δt του ηλεκτρικού φορτίου στο ηλεκτρικό πεδίο.

Β2.Η απόκλιση y του ηλεκτρικού φορτίου από την ευθύγραμμη διάδοσή του τη στιγμή που βγαίνει από το πεδίο.

............................................................

Συνοπτική λύση:

307. Κύλινδρος και …ράβδος σε κεκλιμένο επίπεδο

 

 Ο κύλινδρος του σχήματος έχει μάζα Μ=3Kg και ακτίνα R=10cm. Ο κύλινδρος βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης φ=30⁰ και  ισορροπεί οριακά, ώστε ίσα – ίσα να μην υπερπηδά το εμπόδιο ύψους h=5cm.

Συνοπτική Λύση:

306. Το νήμα χαλαρώνει…

 

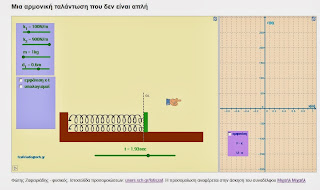
Ο κύβος του σχήματος έχει μάζα Μ  και είναι δεμένος σε ελατήριο σταθεράς Κ και μπορεί να ταλαντώνεται χωρίς τριβές πάνω σε οριζόντιο επίπεδο. Ακόμη ο κύβος Μ είναι δεμένος μέσω μη εκτατού και αβαρούς νήματος μήκους d με σώμα μάζας m. Αρχικά το νήμα είναι τεντωμένο και οριζόντιο και το ελατήριο έχει το φυσικό του. Στη συνέχεια απομακρύνουμε το σύστημα των δυο μαζών μέγιστα κατά Α. Εκείνη τη στιγμή (t=0), αφήνουμε το σύστημα ελεύθερα να κινηθεί και αρχίζει να ταλαντώνεται, τότε: 

Συνοπτική Λύση:

Kaprekar’s Constant.

1. Η σταθερά του Κάπρεκαρ (Kaprekar’s Constant). Η σταθερά, η οποία είναι το 6174, ένας τετραψήφιος αριθμός που έχει μια μοναδική ιδιότητα: "ανεξάρτητα από ποιον τετραψήφιο αριθμό ξεκινάμε (αρκεί να μην είναι όλα τα ψηφία ίδια), μετά από μια σειρά μαθηματικών πράξεων, καταλήγουμε πάντα στο 6174.

 Για παράδειγμα ας ξεκινήσουμε με έναν τετραψήφιο αριθμό, ας πούμε το 3769. Μπορούμε να αναδιατάξουμε τα ψηφία για να σχηματίσουμε τον μεγαλύτερο δυνατό αριθμό και τον μικρότερο δυνατό αριθμό. Στην περίπτωση αυτή, ο μεγαλύτερος δυνατός αριθμός είναι το 9763 και ο μικρότερος δυνατός αριθμός είναι το 3679. Στη συνέχεια αφαιρούμε τον μικρότερο αριθμό από τον μεγαλύτερο αριθμό, 9763–3679 = 6084. Επαναλαμβάνουμε τη διαδικασία με το αποτέλεσμα, 8640–0468 = 8172,

8721-1278=7443

7443-3447=3996

9963-3699=6264

6642-2466=4176

7641-1467=6174.

τελικά φτάνουμε πάντα στον αριθμό 6174  με όποιον τετραψήφιο και να ξεκινήσουμε αρχικά.

.....συνέχεια

305. Περιστροφή ράβδου-m

 

Μια ράβδος ΑΒ, που θεωρείται αβαρής και έχει μήκος L=0,8m μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο, γύρω από άξονα που περνά από το  σημείο της Ο. Το σημείο Ο απέχει από το άκρο της Α απόσταση (ΟΑ)=0,2m. Επίσης στο σημείο Γ της ράβδου με (ΒΓ)=(ΟΑ) υπάρχει στερεωμένη σημειακή μάζα m= 1Kg. Αρχικά η ράβδος ισορροπεί σε κατακόρυφη θέση ώστε το άκρο της Β να βρίσκεται κάτω από τον άξονα περιστροφής.

Μια δεύτερη σημειακή μάζα m, κινείται οριζόντια με σταθερή ταχύτητα υ και συγκρούεται με τη μάζα m που βρίσκεται στο Γ. Αν η κρούση θεωρηθεί ελαστική και ότι η μάζα m τόσο πριν όσο και μετά την κρούση κινείται οριζόντια, τότε να υπολογιστεί η τιμή της ταχύτητας υ, ώστε να πετύχουμε οριακή ανακύκλωση της ράβδου.

Δίνεται g=10m/s².

 

Συνοπτική λύση:

304. Μια παραλλαγή του θέματος Γ (2023).

 Θέμα Γ

Στη διάταξη του διπλανού σχήματος οι κατακόρυφοι μεταλλικοί αγωγοί xx΄, yy΄, αμελητέας ωμικής αντίστασης είναι στερεωμένοι σε οριζόντιο δάπεδο.

Ανάμεσα στα σημεία τους Α και Γ έχει συνδεθεί ιδανικό πηνίο με συντελεστή αυτεπαγωγής L=0,5H.

Μεταλλική ράβδος ZH μήκους ℓ=1m, μάζας m=0,5Kg και ωμικής αντίστασης R=10Ω έχει τα άκρα της πάνω στους κατακόρυφους αγωγούς, είναι κάθετη σε αυτούς και μπορεί να κινείται χωρίς τριβές.  

Στο μέσο της ράβδου και κάθετα σε αυτή ασκείται κατάλληλη δύναμη  με αποτέλεσμα η ράβδος ΖΗ να κινείται προς τα πάνω παραμένοντας συνεχώς οριζόντια με σταθερή ταχύτητα υ=2m/s. Στην περιοχή που κινείται η ράβδος ΖΗ υπάρχει οριζόντιο  ομογενές  μαγνητικό πεδίο έντασης  και μέτρου Β=1Τ, του οποίου οι δυναμικές γραμμές έχουν φορά από τον αναγνώστη προς την σελίδα.

Το πηνίο βρίσκεται έξω από το ομογενές μαγνητικό πεδίο στο οποίο κινείται ο αγωγός ΖΗ. Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη δ και λόγω της κίνησης της ράβδου ο βρόχος ΖΑΓΗΖ διαρρέεται από ρεύμα, i, με φορά όπως αυτή που φαίνεται στο σχήμα.......

Συνοπτική Λύση:

303. Νόμος του Neumann και αυτεπαγωγή.

 

Στο κύκλωμα του σχήματος η ράβδος ΚΛ, έχει ωμική αντίσταση R_ΚΛ=R=1Ω, μήκος L=1m, και μάζα m=0,5Κg. Τη χρονική στιγμή t₀=0 ασκούμε στο μέσο της ράβδου μια σταθερή οριζόντια δύναμη

F­. Τότε η ράβδος 

αρχίζει να ολισθαίνει χωρίς τριβές ενώ βρίσκεται συνέχεια σε επαφή με δυο παράλληλους μεταλλικούς αγωγούς Αx και Ay αμελητέας αντίστασης όπως στο σχήμα. Η ράβδος κινείται μέσα σε ομογενές μαγνητικό πεδίο έντασης (μαγνητικής επαγωγής) Β=1T, που είναι κάθετο στο επίπεδο κίνησης της ράβδου.  Τα άκρα Α και Γ των μεταλλικών αγωγών συνδέονται με ιδανικό πηνίο με συντελεστή αυτεπαγωγής L=0,5H, το οποίο βρίσκεται έξω από το ομογενές μαγνητικό πεδίο. Λόγω της κίνησης της ράβδου ο βρόχος ΚΛΓΑΚ διαρρέεται από ρεύμα Ι=2t. Τότε από τη χρονική στιγμή t₀=0 και μέχρι τη χρονική στιγμή t=2s να υπολογίσετε το συνολικό ηλεκτρικό φορτίο που διέρχεται από μια διατομή του κυκλώματος.

 

Συνοπτική λύση: