242. Ταλάντωση και ιξώδες

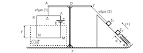
Σώμα μάζας m=2Kg και εμβαδού βάσης S=10^-2m² είναι δεμένο στο ελεύθερο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς Κ=50Ν/m και αρχικά ισορροπεί σε οριζόντιο δάπεδο. Ανάμεσα στο σώμα και στο δάπεδο υπάρχει στρώμα λιπαντικού πάχους L=3mm, το οποίο συμπεριφέρεται ως νευτώνειο ρευστό. Εκτρέπουμε το σώμα από τη θέση ισορροπίας του μέγιστα κατά Α₀=20cm και το αφήνουμε ελεύθερο. Στο σώμα σε όλη τη διάρκεια της κίνησης εξασκείται η δύναμη της εσωτερικής τριβής (ιξώδες) ανάμεσα σε αυτό και το λιπαντικό. Αν ο χρόνος για να γίνει το πλάτος της ταλάντωσης Α= είναι Δt=ln16 s, τότε:

α) Να γράψετε τη σχέση που δείχνει τη μεταβολή του πλάτους της ταλάντωσης σε συνάρτηση με το χρόνο.

β) Να υπολογιστεί ο συντελεστής ιξώδους του λιπαντικού.

γ) Να υπολογιστεί το έργο της δύναμης   ιξώδους στον παραπάνω χρόνο.

δ) Αν κάποια χρονική στιγμή (t=π/15s) η απομάκρυνση του σώματος είναι x=9,5cm και η ταχύτητά του είναι υ=-0,8m/s, τότε να υπολογίσετε την επιτάχυνση του σώματος εκείνη τη στιγμή καθώς και το ρυθμό «απώλειας» ενέργειας. Πόση είναι τότε η «απώλεια» ενέργειας; Να υπολογιστούν επίσης οι ρυθμοί , .

Μια επόμενη χρονική στιγμή που τη θεωρούμε ως αρχή των χρόνων (t₀=0) , που το σώμα περνάει από τη θέση ισορροπίας (x=0) κινούμενο κατά τη θετική φορά (υ>0), εξασκούμε κατάλληλη εξωτερική δύναμη και το σώμα πραγματοποιεί πλέον εξαναγκασμένη αρμονική ταλάντωση με πλάτος ίσο με το Α₀. Αν η μέγιστη ταχύτητα ταλάντωσης του σώματος είναι υ_max=1m/s τότε:

ε) Να γράψετε την εξίσωση της εξωτερικής δύναμης F_εξ σε συνάρτηση με το χρόνο, καθώς και τη χρονική εξίσωση της συνισταμένης δύναμης ΣF.

στ) Αν η εξωτερική συχνότητα του διεγέρτη γίνει ω=4 rad/s, οπότε το πλάτος της εξαναγκασμένης αρμονικής ταλάντωσης γίνεται Α΄=5,4cm για σταθερή μέγιστη εξωτερική δύναμη F₀, ποιες γίνονται τότε οι εξισώσεις F_εξ(t) και ΣF(t); Θεωρείστε για την εξαναγκασμένη αρμονική ταλάντωση αρχική φάση μηδέν.

 Συνοπτική λύση:

ή εδώ