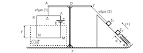
Πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης φ=300 βρίσκεται ένας κύλινδρος μάζας M και ακτίνας R=0,4m. Σε απόσταση r=R/2 από το κέντρο του κυλίνδρου και πάνω σε αυτόν βρίσκεται τυλιγμένο κατάλληλα ένα αβαρές σχοινί χωρίς να γλιστρά.
Το σχοινί περνάει από το αυλάκι μιας σταθερής τροχαλίας μάζας m1 και ακτίνας r1, στο ελεύθερο άκρο του οποίου είναι δεμένο σώμα μάζας m=1Kg. Αν αφήσουμε το σύστημα ελεύθερο αυτό ισορροπεί. Τότε:
Α) Να υπολογιστεί η μάζα Μ του κυλίνδρου.
Β) Τη χρονική στιγμή t0=0 κόβεται το νήμα και ο κύλινδρος αρχίζει να κυλίεται προς τα κάτω στο κεκλιμένο επίπεδο χωρίς να ολισθαίνει με σταθερή επιτάχυνση μέτρου αcm=10/3m/s2. Τότε τη χρονική στιγμή t=3s να υπολογιστούν:
α) Ο ρυθμός μεταβολής της ορμής του κυλίνδρου καθώς και η ταχύτητα υΑ του σημείου επαφής του κυλίνδρου με το κεκλιμένο επίπεδο.
β) Η ταχύτητα υΒ και η συνολική επιτάχυνση αΒ ενός σημείου Β της κάθετης στο κεκλιμένο επίπεδο διαμέτρου του, που απέχει απόσταση r από το κέντρο Κ του κυλίνδρου.
γ) η συνολική ταχύτητα υΓ του σημείου Γ που βρίσκεται σε απόσταση r από το κέντρο Κ του κυλίνδρου κατά μήκος μιας διαμέτρου του παράλληλης στο κεκλιμένο επίπεδο, καθώς και η συνολική επιτάχυνση του Γ η παράλληλη στο κεκλιμένο επίπεδο.
Γ) Αν η μάζα m, διανύει απόσταση L=80cm και συγκρούεται πλαστικά με μάζα m2=1Kg που πραγματοποιεί α.α.τ με εξίσωση x=ημ(5t) (S.I) και εκείνη τη στιγμή βρίσκεται στη θέση ισορροπίας της, κινούμενη προς τη θετική κατεύθυνση, τότε να βρείτε
α) Το ρυθμό μεταβολής της κινητικής ενέργειας της μάζας m τη στιγμή της σύγκρουσης και
β) την εξίσωση της α.α.τ του συσσωματώματος μετά την πλαστική κρούση.
Δίνεται g=10m/s2.















Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου