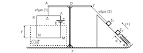
Το ενιαίο στερεό του σχήματος αποτελείται από μια λεπτή ομογενή και ισοπαχή ράβδο ΑΒ, μήκους L=1m και μάζας Μ=3Kg, και από ένα λεπτό ομογενή δίσκο ακτίνας (OB)=r=0,4 m και μάζας m=1Kg.
Η ράβδος ΑΒ εφάπτεται στο δίσκο, ο οποίος είναι κολλημένος στο άκρο Β της ράβδου όπως φαίνεται στο σχήμα,
σχηματίζοντας ένα ενιαίο στερεό.
Το σύστημα αρχικά συγκρατείται στη θέση όπου η ράβδος ΑΒ είναι οριζόντια.
Τότε:
α) Να υπολογιστεί η συνολική ροπή αδράνειας της διάταξης ως προς το σημείο Α.
β) Να υπολογιστεί ο ρυθμός μεταβολής της στροφορμής του συστήματος των σωμάτων,
i) τη στιγμή που αφήνουμε το σύστημα από την αρχική του θέση να περιστραφεί.
ii) όταν η ράβδος γίνει κατακόρυφη
γ) i) Να υπολογιστεί η ολική κινητική ενέργεια της διάταξης μόλις η ράβδος γίνει κατακόρυφη.
ii) Να υπολογιστεί εκείνη τη στιγμή ο λόγος των κινητικών ενεργειών , όπου Κρ είναι η κινητική ενέργεια της ράβδου και Κδ είναι η κινητική ενέργεια του δίσκου.
δ) Να υπολογιστεί η ολική κινητική ενέργεια της διάταξης μόλις η ράβδος περιστραφεί από την αρχική οριζόντια θέση της κατά φ=600. Πόσος είναι τότε ο ρυθμός μεταβολής της στροφορμής του συστήματος των σωμάτων;
Δίνεται η ροπή αδράνειας της ράβδου ως προς το κέντρο μάζας της Icm= ΜL2, η ροπή αδράνειας του δίσκου ως προς το κέντρο μάζας του Ιο= mr2 και =1,7.Συνοπτική λύση:
ή εδώ
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου