291. Σύστημα ράβδων

 

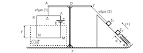
Δυο λεπτές ομογενείς και ισοπαχείς ράβδοι ΑΒ και ΒΓ, από το ίδιο υλικό, έχουν συγκολληθεί κάθετα μεταξύ τους στο άκρο τους Β. Η ράβδος ΑΒ έχει μήκος

L₁=1m και μάζα m₁=3Kg, ενώ η ράβδος ΒΓ έχει μήκος L₂=0,5m. Στο άκρο Γ της ράβδου ΒΓ έχει συγκολληθεί σημειακή μάζα m=0,5Kg, όπως φαίνεται στο σχήμα. Το σύστημα των τριών μαζών μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον άξονα ZZ΄ που περνά από το σημείο Α και είναι κάθετος στο επίπεδο περιστροφής της ΑΒ και παράλληλος με τη ΒΓ. Τότε:

 Α) Να υπολογιστεί η ολική ροπή αδράνειας του συστήματος ως προς τον άξονα ΖΖ΄.

Β) Αν μια δεύτερη σημειακή μάζα m΄=m, κινείται σε οριζόντια κυκλική τροχιά κέντρου πάνω στον ΖΖ΄ και ακτίνας L₁ με σταθερό μέτρο ταχύτητας υ=7m/s και συγκρούεται κεντρικά και ελαστικά με τη μάζα m, τότε να βρεθεί η γωνιακή ταχύτητα ω, του συστήματος των m₁,m₂ και m αμέσως μετά την κρούση.

 Γ) Αν κάποια χρονική στιγμή (t₀=0) μετά την κρούση,  εφαρμόσουμε κάθετα στο μέσο M της ΑΒ, σταθερή κατά μέτρο δύναμη F=N, με φορά αντίθετη τη περιστροφής τότε να βρείτε:

i) το μέτρο της επιτάχυνσης του σημείου M, αμέσως μετά την εφαρμογή της δύναμης F,

ii) τη γωνία στροφής της ΑΒ μέχρι να σταματήσει η περιστροφή του συστήματος,

iii) το χρόνο για να σταματήσει η περιστροφή του συστήματος,

iv) το έργο W της δύναμης F, από τη χρονική στιγμή t₀=0 και μέχρι να σταματήσει η περιστροφή.

Δ)i)Να υπολογιστεί ο ρυθμός μεταβολής της στροφορμής του συστήματος των m₁,m₂ και m καθώς και της ράβδου ΒΓ.

 ii) Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας του συστήματος

αμέσως μετά την κρούση.

 Συνοπτική 
Λύση