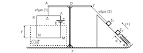
Γύρω από τον ομογενή τροχό
του σχήματος μάζας m=4Κg και ακτίνας R, είναι τυλιγμένο πολλές
φορές ένα αβαρές νήμα. Το ελεύθερο άκρο του νήματος δένεται με σώμα μάζας M=1Kg. Τη χρονική στιγμή t0=0 αφήνουμε τον τροχό
ελεύθερο να κινηθεί. Ο τροχός κυλίεται
χωρίς να ολισθαίνει πάνω στο κεκλιμένο επίπεδο γωνίας κλίσης φ=300.
Αν η Μ ολισθαίνει στο κεκλιμένο
επίπεδο και ο συντελεστής τριβής ολίσθησης ανάμεσα στο κεκλιμένο επίπεδο και τη
μάζα Μ είναι μ, τότε:
α) Να υπολογιστεί η επιτάχυνση του
κέντρου μάζας της m.
β) Αν το αρχικό μήκος του νήματος είναι L=1m τότε σε πόσο χρόνο t1 θα συγκρουστούν τα δύο
σώματα;
γ) Να υπολογιστεί ο ρυθμός
μεταβολής της κινητικής ενέργειας της κάθε μια μάζας, καθώς και του συστήματος τους
τη χρονική στιγμή t2=t1/2,
δ) Να υπολογιστεί ο ρυθμός
μεταβολής της στροφορμής της κάθε μια μάζας καθώς και του συστήματος τους ως
προς το σημείο Α του κεκλιμένου επιπέδου, αν δίνεται η ακτίνα του τροχού R=0,1m.
Δίνεται για τον τροχό Ιcm=mR2 και g=10m/s2. Ακόμη οι διαστάσεις του Μ είναι τέτοιες ώστε για τις συνθήκες του προβλήματος να μην ανατρέπεται.
Δίνεται για τον τροχό Ιcm=mR2 και g=10m/s2. Ακόμη οι διαστάσεις του Μ είναι τέτοιες ώστε για τις συνθήκες του προβλήματος να μην ανατρέπεται.
Συνοπτική λύση:















Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου